Vectores
Nombre: Paola Llerena
Curso: 2do BGU "B"
Definicion
Un vector puede utilizarse para representar una magnitud física, quedando definido por un módulo y una dirección u orientación. Su expresión geométrica consiste en segmentos de recta dirigidos hacia un cierto lado, asemejándose a una flecha. La velocidad y la fuerza son dos ejemplos de magnitudes vectoriales.
Dentro de este ámbito científico, y también de las Matemáticas, se hace necesario dejar patente que existe una gran variedad de vectores. De tal manera, que podemos hablar de fijos, paralelos, deslizantes, opuestos, concurrentes, libres o colineales, entre otros muchos más
Gráficamente, un vector se representa como una flecha ubicada en un eje de coordenadas. En esta flecha podemos identificar cada uno de los elementos que lo conforman y que estudiamos en el apartado anterior, además de algunos más.
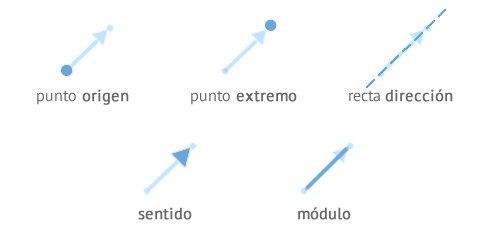
- Tienen un punto desde el que nace la flecha llamado origen o punto de aplicación.
- De igual forma, tienen otro punto donde termina la flecha llamado extremo.
- La recta sobre la que "descansan" los puntos de extremo y origen se denomina dirección o recta soporte.
- La distancia entre el punto origen y extremo corresponde con su módulo. A mayor distancia entre ellos, el módulo será mayor.
- La punta de la flecha determina su sentido, dentro de los dos posibles que se podría dibujar siguiendo su dirección, es decir hacia un lado de la recta o hacia el otro.
Componentes de un vector
En un sistema coordenado de dos dimensiones, cualquier vector puede separarse en elcomponente x y el componente y.
Por ejemplo, en la figura siguiente mostrada, el vector  se separa en dos componentes, vx y vy . Digamos que el ángulo entre el vector y su componente x es θ.
se separa en dos componentes, vx y vy . Digamos que el ángulo entre el vector y su componente x es θ.
El vector y sus componentes forman un triángulo rectángulo como se muestra a continuación.
En la figura anterior, los componentes pueden leerse rápidamente. El vector en la forma componente es  .
.
Las relaciones trigonométricas dan la relación entre la magnitud del vector y los componentes del vector.
vx = v cos θ
vy = v sin θ
Usando el Teorema de Pitágoras en el triángulo rectángulo con longitudes vx y vy:
Aquí, los números mostrados son las magnitudes de los vectores.
Caso 1: Dados los componentes de un vector, encuentre la magnitud y la dirección del vector.
Use las fórmulas siguientes en este caso.
La magnitud del vector es  .
.
Para encontrar la dirección del vector, resuelva  for θ.
for θ.
Caso 2: Dada la magnitud y la dirección de un vector, encuentre los componentes del vector.
Use las fórmulas siguientes en este caso.
vx = v cos θ
vy = v sin θ
Video
No hay comentarios:
Publicar un comentario